- Auteur admin caroline@plants-knowledge.com.
- Public 2023-12-17 03:37.
- Laatst gewijzigd 2025-06-01 06:48.
Omgebouwde ruimte en woonruimte zijn twee van de belangrijkste parameters die herhaaldelijk worden gebruikt om een gebouw in een breed scala aan vakgebieden te definiëren. Hoewel de woonruimte vrij eenvoudig kan worden bepaald, levert de cubatuur altijd problemen op. Wat houdt dit in en wat wordt in de berekening verwaarloosd? Wij leggen stap voor stap uit hoe u veilig een betrouwbaar resultaat kunt bereiken.
Wat is de cubatuur?
De term ‘cubature’ komt van het Latijnse ‘cubus’ en beschrijft rechtstreeks een lichaam. In het geval van gebouwen verruimt dit lichaam echter de definitie en verwijst het naar het volume dat de woning als geheel in beslag neemt. Over het algemeen omvat dit de som van de verschillende volumes die samen het totale volume vormen:
- Nettovolume: Volume van alle bruikbare kamers, “luchtvolume” in het gebouw
- Bouwvolume: Volume van alle componenten van een gebouw, d.w.z. muren, plafonds, dak, enz.
Hoewel cubature nog steeds alomtegenwoordig is in technisch taalgebruik, is de modernere uitdrukking ‘omgebouwde ruimte’ te vinden in de huidige regelgeving, die in principe hetzelfde beschrijft.
Wat is het doel van een verbouwde kamer?
Leken vragen zich altijd af waarom er zoveel ophef wordt gemaakt over de berekening van de cubatuur. Een blik op de diverse toepassingen van deze waarde maakt de betekenis ervan snel duidelijk:
- Kostenplanning en monitoring
- Indicator voor juridische beoordeling van bouwplanning
- Bouwfinanciering
- Basis voor het bepalen van de reële waarde
- Individuele aspecten
LET OP:
Je leest steeds weer over de zogenaamde “bouwmassa” in de vakliteratuur, jurisprudentie en regelgeving. Afhankelijk van het stel regels kan de bepaling enigszins variëren, maar uiteindelijk gaat het ook om het volume of de omsloten ruimte.
DIN277-1 als basis voor berekening
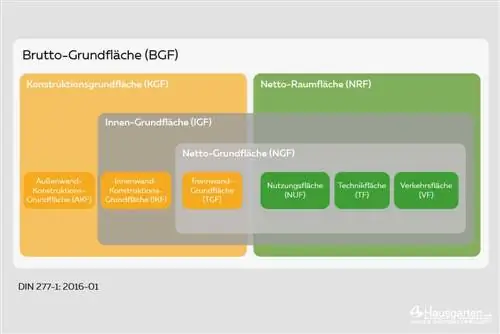
In tegenstelling tot de bepaling van de woon- of gebruiksoppervlakte, waarbij meerdere bepalingsmethoden gelijkwaardig beschikbaar zijn, is de basis voor de berekening van de kubus duidelijk en eenvoudig. In Duitsland bestaat er een bindende set regels die alle specificaties bevat voor het bepalen van de kubus: DIN 277-1 "Basisoppervlakken en volumes in de bouw - Deel 1: Bouwconstructie". Deze regeling gaat zelfs terug tot 1934, toen voor het eerst een uniforme bepaling werd gedaan om het volume te bepalen, wat toen officieel cuture werd genoemd. Na verschillende wijzigingen en herzieningen is vandaag de dag de huidige versie van deze DIN-norm uit 2016 van toepassing.
LET OP:
Hoewel DIN 277-1 geen wet is, maar eerder een norm die niet algemeen toepasbaar is, wordt deze nu algemeen erkend en daarom vrijwel bindend. Als technische regel behoort het nu tot de erkende stand van de techniek en wordt het ook door rechtbanken als referentie gebruikt in geval van een geschil. Als besloten ruimte anders wordt berekend, is dat mogelijk, maar in geval van een geschil vergt dit een enorme inspanning om de gelijkwaardigheid te rechtvaardigen en te bewijzen.
Waar wordt rekening mee gehouden en wat wordt weggelaten?
Een blik op de DIN maakt snel duidelijk wat tot de cubature behoort en wat niet. De inleidende zin van artikel 7 “Bepaling van de inhoud van het gebouw” vermeldt duidelijk de essentiële inhoud:
“De bruto volumetrische inhoud (GRI) omvat het volume van alle kamers en gebouwconstructies die zich boven het bruto vloeroppervlak (BVO) van het gebouw bevinden.”
Er wordt verder gedefinieerd dat het brutovolume, een ander synoniem voor omsloten ruimte of kubus, wordt gevormd door de buitenste grensvlakken van gebouwbases, buitenmuren en daken met dakkapellen. Simpel gezegd betekent dit dat het dakvlak, de buitenrand van de gevel en de vloerplaat de begrenzing vormen van het beschouwde volume. Nu rijst terecht de vraag hoe dit in detail zal worden aangepakt. In individuele gevallen heeft een huis een groot aantal details die, afhankelijk van de interpretatie van de DIN, al dan niet tot extra volume kunnen leiden. Om hier duidelijkheid te verschaffen is duidelijk geregeld welke bouwdelen expliciet niet worden meegenomen in de kubusberekening:
- Diepe en ondiepe funderingen, d.w.z. funderingen en vloerplaten
- Lichtschachten
- Externe trappen en hellingen als ze niet structureel verbonden zijn met het gebouw
- Ingangsluifels
- Dakoverstekken
- Vrijdragende zonweringsystemen
- Schoorstenen, afvoer- en ventilatiepijpen die boven de dakbedekking uitsteken
- Lichtkoepels met een volume boven het dakmembraan van maximaal één kubieke meter
- Pergola's
- Stevige zitplaatsen of terrassen buiten, zelfs als ze boven de grond uitsteken
Het speciale geval
Delen van een gebouw die niet volledig omsloten zijn, nemen een enigszins bijzondere positie in bij de volumeberekening. Voorbeelden hiervan zijn daken op steunen die geen gesloten wanden hebben. Ook vaak aangetroffen zijn zolders of balkonboringen, d.w.z. verticale muursegmenten waarbij de bovenste “afdekking” in de vorm van een dak ontbreekt. Hier stelt de DIN duidelijk dat zogenaamde fictieve componenten kunnen en moeten worden gebruikt om de ruimte af te bakenen.
Wat betekent dit?
Dit betekent eenvoudigweg dat de bovenrand van een zolder de bovengrens vertegenwoordigt van het op deze manier gevormde volume. In het geval van een dak worden de fictieve buitenmuren gedefinieerd door de steunen of - indien uitkragend zonder steunen - door de rand van het dak.
LET OP:
Het afbakenen van de dakrand en het dak is niet zo eenvoudig, omdat een bepaald gedeelte van de dakrand vaak vergroot wordt en zo de terrasoverkapping vormt. Hier kunt u normaal gesproken een grens van 0,50 meter hanteren. Indien een dakoverstek groter is, wordt gesproken van een ruimtevormend dak. Tot 0,50 meter is dit een dakrand waar geen rekening mee wordt gehouden.
De berekening aan de hand van het voorbeeld stap voor stap

Laten we nu eens kijken naar de volumeberekening aan de hand van een concreet voorbeeld. Als object van onze volumebepaling beschouwen we een typische eengezinswoning met de volgende kenmerken:
- Lengte 10 meter
- Breedte 8,5 meter
- Eave height (hoogte van snijpunt buitenmuur met dakbedekking=vanaf terrein 3, 50 meter
- nokhoogte 6,00 meter
- Kelder, bovenrand vloerplaat 3,00 meter onder de grond
- Dakvorm zadeldak
- Dakoverstek 0, 30 meter
- Bijlage vestibule 1, 00 meter breed, 1, 50 meter diep, vanaf de grond 3, 00 meter hoog, plat dak
- Uitbreiding terrasdak, steunafstand 3,00 meter vanaf de rand van het huis en 3,00 meter breed, plat dak, hoogte vanaf de grond 2,50 meter
Stap voor stap
1. Mentale ontbinding in tastbare deelvolumes:
- Huislichaam, bovenrand van de vloerplaat tot dakrandhoogte
- Dakrandhoogte tot nokhoogte
- voorruit
- Terrasoverkapping
2. Bepaling van de wiskundige formules voor de volumeberekening van de onderstructuren:
a. Huislichaam: Lengte x breedte x hoogte
b. Dak: Lengte x breedte x hoogte x 0,5
c. Windvanger: Lengte x breedte x hoogte
d. Terrasoverkapping: Lengte x breedte x hoogte
3. Berekening van volume:
a. Huislichaam: 10, 00m x 8, 50m x (3, 50m+3, 00m)=552, 50m³
b. Dak: 10,00 m x 8,50 m x (6,00 m - 3,50 m) x 0,5=212,00 m³
c. Windscherm: 1,50 m x 1,00 m x 3,00 m=4,50 m³
d. Terrasoverkapping: 3,00m x 3,00m x 2,50m=22,50m³
e. Som a. tot d.=791, 50m³
Opmerkingen over berekening
Het voorbeeld laat zien dat het berekenen van een cubatuur eigenlijk heel eenvoudig is met de juiste aanpak. Met deze hints en tips kunt u uw doel zonder fouten bereiken:
Dissectie

Breek de te berekenen structuur op in afzonderlijke volumes die zo eenvoudig mogelijk te berekenen zijn. Dit betekent dat je vrijwel altijd de formules voor kubusvormige of driehoekige lichamen kunt gebruiken die je uit je schooltijd kent.
Dakhelling
Hoe steil een dak ook is en of het nu een symmetrisch of asymmetrisch dak is, schuine daken kunnen altijd worden berekend met de formule lengte x breedte x hoogte x 0,5. Zelfs enkelvoudige daken kunnen op deze manier worden berekend als je het opvat als een speciale vorm van zadeldak met een dakoppervlak met een helling van 90 graden.
Onderrand voor speciale componenten
Of het nu gaat om een vestibule of een terrasoverkapping, wanneer er geen structurele onderrand is, kan het terreinoppervlak worden gezien als de ondergrens van het volume. Als een vestibule zich bijvoorbeeld op hellend terrein bevindt, gebruik dan de hoogte van het terrein ter hoogte van de toegangsdeur als relevante hoogte.






